
HL Paper 2
This question is in two parts. Part 1 is about gravitational force fields. Part 2 is about properties of a gas.
Part 1 Gravitational force fields
State Newton’s universal law of gravitation.
A satellite of mass m orbits a planet of mass M. Derive the following relationship between the period of the satellite T and the radius of its orbit R (Kepler’s third law).
\({T^2} = \frac{{4{\pi ^2}{R^3}}}{{GM}}\)
A polar orbiting satellite has an orbit which passes above both of the Earth’s poles. One polar orbiting satellite used for Earth observation has an orbital period of 6.00 × 103s.
Mass of Earth = 5.97 × 1024 kg
Average radius of Earth = 6.37 × 106 m
(i) Using the relationship in (b), show that the average height above the surface of the Earth for this satellite is about 800 km.
(ii) The satellite moves from an orbit of radius 1200 km above the Earth to one of radius 2500 km. The mass of the satellite is 45 kg.
Calculate the change in the gravitational potential energy of the satellite.
(iii) Explain whether the gravitational potential energy has increased, decreased or stayed the same when the orbit changes, as in (c)(ii).
Markscheme
the (attractive) force between two (point) masses is directly proportional to the product of the masses;
and inversely proportional to the square of the distance (between their centres of mass);
Use of equation is acceptable:
Award [2] if all five quantities defined. Award [1] if four quantities defined.
\(G\frac{{Mm}}{{{R^2}}} = \frac{{m{v^2}}}{R}\) so \({v^2} = \frac{{Gm}}{R}\);
\(v = \frac{{2\pi R}}{T}\);
\({v^2} = \frac{{4{\pi ^2}{R^2}}}{{{T^2}}} = \frac{{Gm}}{R}\);
or
\(G\frac{{Mm}}{{{R^2}}} = m{\omega ^2}R\);
\({\omega ^2} = \frac{{4{\pi ^2}}}{{{T^2}}}\);
\(\frac{{4{\pi ^2}}}{{{T^2}}} = \frac{{GM}}{{{R^3}}}\);
Award [3] to a clear response with a missing step.
(i) \({R^3} = \frac{{6.67 \times {{10}^{ - 11}} \times 5.97 \times {{10}^{24}} \times {{6000}^2}}}{{4 \times {\pi ^2}}}\);
R=7.13x106(m);
h=(7.13x106-6.37x106)=760(km);
Award [3] for an answer of 740 with π taken as 3.14.
(ii) clear use of \(\Delta V = \frac{{\Delta E}}{m}\) and \(V = - \frac{{Gm}}{r}\) or \(\Delta E = GMm\left( {\frac{1}{{{r_1}}} - \frac{1}{{{r_2}}}} \right)\);
one value of potential energy calculated (2.37×109 or 2.02×109 );
3.5×108 (J);
Award [3] for a bald correct answer.
Award [2] for 7.7x109. Award [1] for 7.7x1012.
Award [0] for answers using mgΔh.
(iii) increased;
further from Earth / closer to infinity / smaller negative value;
Award [0] for a bald correct answer.
Examiners report
(a) Many candidates stated that the Newton’s law force is proportional to the masses of the objects in question, rather than the product of the masses.
This part was generally well done with most candidates coming to the correct outcome; too often steps were missed out in the derivations and this cost candidates mark. It is essential that they realise that a derivation must include every step. The presentation of this part left much to be desired in quite a large minority with mathematically incorrect statements being given.
(i) Most candidates were able to substitute values into the equation and rearrange it to find a value for R. Many then fail to subtract the radius of the Earth.
(ii) Very few candidates completed this part correctly. Confusion between potential and potential energy was common as were adding the height in kilometres to the radius of the Earth in metres. A sizeable minority of candidates attempted to use the mgh equation.
(iii) This part was quite well answered with most candidates realising that the increase in height meant an increase in potential energy. Several argued that the magnitude decreased but being a negative quantity this meant an increase.
This question is about the thermodynamics of a car engine and the dynamics of the car.
A car engine consists of four cylinders. In each of the cylinders, a fuel-air mixture explodes to supply power at the appropriate moment in the cycle.
The diagram models the variation of pressure P with volume V for one cycle of the gas, ABCDA, in one of the cylinders of the engine. The gas in the cylinder has a fixed mass and can be assumed to be ideal.
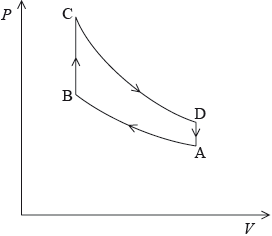
The car is travelling at its maximum speed of \({\text{56 m}}\,{{\text{s}}^{ - 1}}\). At this speed, the energy provided by the fuel injected into one cylinder in each cycle is 9200 J. One litre of fuel provides 56 MJ of energy.
A car is travelling along a straight horizontal road at its maximum speed of \({\text{56 m}}\,{{\text{s}}^{ - 1}}\). The power output required at the wheels is 0.13 MW.
A driver moves a car in a horizontal circular path of radius 200 m. Each of the four tyres will not grip the road if the frictional force between a tyre and the road becomes less than 1500 N.
At point A in the cycle, the fuel-air mixture is at 18 °C. During process AB, the gas is compressed to 0.046 of its original volume and the pressure increases by a factor of 40. Calculate the temperature of the gas at point B.
State the nature of the change in the gas that takes place during process BC in the cycle.
Process CD is an adiabatic change. Discuss, with reference to the first law of thermodynamics, the change in temperature of the gas in the cylinder during process CD.
Explain how the diagram can be used to calculate the net work done during one cycle.
(i) Calculate the volume of fuel injected into one cylinder during one cycle.
(ii) Each of the four cylinders completes a cycle 18 times every second. Calculate the distance the car can travel on one litre of fuel at a speed of \({\text{56 m}}\,{{\text{s}}^{ - 1}}\).
A car accelerates uniformly along a straight horizontal road from an initial speed of \({\text{12 m}}\,{{\text{s}}^{ - 1}}\) to a final speed of \({\text{28 m}}\,{{\text{s}}^{ - 1}}\) in a distance of 250 m. The mass of the car is 1200 kg. Determine the rate at which the engine is supplying kinetic energy to the car as it accelerates.
(i) Calculate the total resistive force acting on the car when it is travelling at a constant speed of \({\text{56 m}}\,{{\text{s}}^{ - 1}}\).
(ii) The mass of the car is 1200 kg. The resistive force F is related to the speed v by \(F \propto {v^2}\). Using your answer to (g)(i), determine the maximum theoretical acceleration of the car at a speed of \({\text{28 m}}\,{{\text{s}}^{ - 1}}\).
(i) Calculate the maximum speed of the car at which it can continue to move in the circular path. Assume that the radius of the path is the same for each tyre.
(ii) While the car is travelling around the circle, the people in the car have the sensation that they are being thrown outwards. Outline how Newton’s first law of motion accounts for this sensation.
Markscheme
535 (K) / 262 (°C);
constant volume change / isochoric / isovolumetric / OWTTE;
Q/thermal energy transfer is zero;
\(\Delta U = - W\);
as work is done by gas internal energy falls;
temperature falls as temperature is measure of average kinetic energy;
work done is estimated by evaluating area;
inside the loop / OWTTE;
(i) \(1.6 \times {10^{ - 4}}{\text{ (litre)}}\);
(ii) one litre \( = \left( {\frac{1}{{4 \times 18 \times 1.64 \times {{10}^{ - 4}}}} = } \right){\text{ }}87{\text{ s of travel}}\);
\((87 \times 56) = 4.7{\text{ (km)}}\);
Allow rounded 1.6 value to be used, giving 4.9 (km).
use of a kinematic equation to determine motion time \({\text{(}} = 12.5{\text{ s)}}\);
change in kinetic energy \( = \frac{1}{2} \times {\text{1200}} \times {\text{[2}}{{\text{8}}^2} - {\text{1}}{{\text{2}}^2}]{\text{ (}} = 384{\text{ kJ)}}\);
rate of change in kinetic energy \( = \frac{{{\text{384000}}}}{{{\text{12.5}}}}\); } (allow ECF of 162 from (28 \( - \) 12)2 for this mark)
31 (kW);
or
use of a kinematic equation to determine motion time \(( = 12.5{\text{ s)}}\);
use of a kinematic equation to determine acceleration \(( = 1.28{\text{ m}}\,{{\text{s}}^{ - 2}})\);
work done \(\frac{{F \times s}}{{{\text{time}}}} = \frac{{1536 \times 250}}{{12.5}}\);
31 (kW);
(i) \({\text{force}} = \frac{{{\text{power}}}}{{{\text{speed}}}}\);
2300 or 2.3k (N);
Award [2] for a bald correct answer.
(ii) resistive force \( = \frac{{2300}}{4}\)\(\,\,\,\)or\(\,\,\,\)\(\frac{{2321}}{4}{\text{ }}( = {\text{575)}}\); (allow ECF)
so accelerating force \((2300 - 580 = ){\text{ }}1725{\text{ (N)}}\)\(\,\,\,\)or\(\,\,\,\)1741 (N);
\(a = \frac{{1725}}{{1200}} = 1.44{\text{ (m}}\,{{\text{s}}^{ - 2}})\)\(\,\,\,\)or\(\,\,\,\)\(a = \frac{{1741}}{{1200}} = 1.45{\text{ (m}}\,{{\text{s}}^{ - 2}})\);
Award [2 max] for an answer of 0.49 (m\(\,\)s–2 (omits 2300 N).
(i) centripetal force must be \( < 6000{\text{ (N)}}\); (allow force 6000 N)
\({v^2} = F \times \frac{r}{m}\);
\(31.6{\text{ (m}}\,{{\text{s}}^{ - 1}})\);
Allow [3] for a bald correct answer.
Allow [2 max] if 4\( \times \) is omitted, giving 15.8 (m\(\,\)s–1).
(ii) statement of Newton’s first law;
(hence) without car wall/restraint/friction at seat, the people in the car would move in a straight line/at a tangent to circle;
(hence) seat/seat belt/door exerts centripetal force;
(in frame of reference of the people) straight ahead movement is interpreted as “outwards”;
Examiners report
This simple gas law calculation was surprisingly badly done. Certainly similar questions have attracted better scores in previous examinations. Common errors included the inevitable failure to work in kelvin, and simple arithmetic errors.
Most candidates were able to describe the constant volume nature of the change in question.
Many candidates scored full credit in a question that has been well rehearsed in previous examinations. The zero change in thermal energy transfer was common and many were able to deduce that \(\Delta U\) is therefore equal to \( - W\). This led immediately to a deduction of temperature decrease.
Almost all recognised that the work done was related to some area under the graph. In a small minority of cases the exact specification of the area was too imprecise to gain the second mark.
(i) It was common to see a correct value for the volume of fuel used though not a correct unit.
(ii) Many were able to arrive at a travel time for the fuel and therefore the distance travelled. However, routes were indirect and lengthy and few could see a direct way to the answer.
There were at least two routes to tackle this problem. Some solutions were so confused that it was difficult to decide which method had been used. Common errors included: forgetting that the initial speed was \({\text{12 m}}\,{{\text{s}}^{ - 1}}\) not zero, power of ten errors, and simple mistakes in the use of the kinematic equations, or failure to evaluate work done \( = {\text{force }} \times {\text{ distance}}\) correctly. However, many candidates scored partial credit. Scores of two or three out of the maximum four were common showing that many are persevering to get as far as they can.
(i) Many correct solutions were seen. Candidates are clearly comfortable with the use of the equation force = power/speed.
(ii) The method to be used here was obvious to many. What was missing was a clear appreciation of what was happening in terms of resistive force in the system. Many scored two out of three because they indicated a sensible method but did not use the correct value for the force. Scoring two marks does require that the explanation of the method is at least competent. Those candidates who give limited explanations of their method leading to a wrong answer will generally accumulate little credit. A suggestion (never seen in answers) is that candidates should have begun from a free-body force diagram which would have revealed the relationship of all the forces.
(i) The major problem here was that most candidates did not recognise that 1500 N of force acting at each of four wheels will imply a total force of 6 kN. Again, partial credit was available only if it was clear what the candidate was doing and what the error was.
(ii) Statements of Newton’s first law were surprisingly poor. As in previous examinations, few candidates appear to have learnt this essential rule by heart and they produce a garbled and incomplete version under examination pressure. The first law was then only loosely connected to the particular context of the question. Candidates have apparently not learnt to relate the physics they learn to everyday contexts.
This question is in two parts. Part 1 is about fields, electric potential difference and electric
circuits. Part 2 is about thermodynamic cycles.
Part 1 Fields, electric potential difference and electric circuits
The magnitude of gravitational field strength g is defined from the equation shown below.
\[g = \frac{{{F_g}}}{m}\]
The magnitude of electric field strength E is defined from the equation shown below.
\[E = \frac{{{F_E}}}{q}\]
For each of these defining equations, state the meaning of the symbols
(i) Fg.
(ii) FE.
(iii) m.
(iv) q.
In a simple model of the hydrogen atom, the electron is regarded as being in a circular orbit about the proton. The magnitude of the electric field strength at the electron due to the proton is Ep . The magnitude of the gravitational field strength at the electron due to the proton is gp.
Determine the order of magnitude of the ratio shown below.
\[\frac{{{E_p}}}{{{g_p}}}\]
Markscheme
(i) the force exerted on a small/test/point mass;
Do not allow bald “gravitational force”.
(ii) the force exerted on a small/point/test positive charge;
To award [1] “positive” is required.
Do not allow bald “electric force”.
(iii) the size/magnitude/value of the small/point mass;
Do not accept bald “mass”.
(iv) the magnitude/size/value of the small/point/test (positive) charge;
Do not accept bald “charge”.
In part (a) only penalize lack of “small/test/point” once, annotate as ECF.
It must be clear that the mass/charge in (iii) & (iv) refer to the object in (i) and (ii).
\({E_p} = \frac{e}{{4\pi {\varepsilon _0}{r^2}}}\) and \({g_p} = \frac{{G{m_p}}}{{{r^2}}}\); (both needed)
\(\frac{e}{{4\pi {\varepsilon _0}G{m_p}}}\left( { = \frac{{9 \times {{10}^9} \times 1.6 \times {{10}^{ - 19}}}}{{6.7 \times {{10}^{ - 11}} \times 1.7 \times {{10}^{ - 27}}}}} \right)\);
≈1028;
Award [2 max] if response calculates ratio of force as this is an ECF from the first marking point (1039) .
Award [3] for solution that correctly evaluates field strengths separately and then divides.
Examiners report
In this part candidates were completely at a loss and could not state the meanings of the symbols in the definitions of gravitational or electric field strengths. This was a disappointing failure in what was meant to be an easy opener to the whole question.
Following (a) candidates failed widely on this part too. They often had little idea which data to use (mass and charge were frequently confused) and sometimes the meaning of the constants in the equations failed them too. This was compounded by arithmetic errors to make a straightforward calculation very hard for many.
The gravitational potential due to the Sun at its surface is –1.9 x 1011 J kg–1. The following data are available.
| Mass of Earth | = 6.0 x 1024 kg |
| Distance from Earth to Sun | = 1.5 x 1011 m |
| Radius of Sun | = 7.0 x 108 m |
Outline why the gravitational potential is negative.
The gravitational potential due to the Sun at a distance r from its centre is VS. Show that
rVS = constant.
Calculate the gravitational potential energy of the Earth in its orbit around the Sun. Give your answer to an appropriate number of significant figures.
Calculate the total energy of the Earth in its orbit.
An asteroid strikes the Earth and causes the orbital speed of the Earth to suddenly decrease. Suggest the ways in which the orbit of the Earth will change.
Outline, in terms of the force acting on it, why the Earth remains in a circular orbit around the Sun.
Markscheme
potential is defined to be zero at infinity
so a positive amount of work needs to be supplied for a mass to reach infinity
VS = \( - \frac{{GM}}{r}\) so r x VS «= –GM» = constant because G and M are constants
GM = 1.33 x 1020 «J m kg–1»
GPE at Earth orbit «= –\(\frac{{1.33 \times {{10}^{20}} \times 6.0 \times {{10}^{24}}}}{{1.5 \times {{10}^{11}}}}\)» = «–» 5.3 x 1033 «J»
Award [1 max] unless answer is to 2 sf.
Ignore addition of Sun radius to radius of Earth orbit.
ALTERNATIVE 1
work leading to statement that kinetic energy \(\frac{{GMm}}{{2r}}\), AND kinetic energy evaluated to be «+» 2.7 x 1033 «J»
energy «= PE + KE = answer to (b)(ii) + 2.7 x 1033» = «–» 2.7 x 1033 «J»
ALTERNATIVE 2
statement that kinetic energy is \( = - \frac{1}{2}\) gravitational potential energy in orbit
so energy «\( = \frac{{{\text{answer to (b)(ii)}}}}{2}\)» = «–» 2.7 x 1033 «J»
Various approaches possible.
«KE will initially decrease so» total energy decreases
OR
«KE will initially decrease so» total energy becomes more negative
Earth moves closer to Sun
new orbit with greater speed «but lower total energy»
changes ellipticity of orbit
centripetal force is required
and is provided by gravitational force between Earth and Sun
Award [1 max] for statement that there is a “centripetal force of gravity” without further qualification.
Examiners report
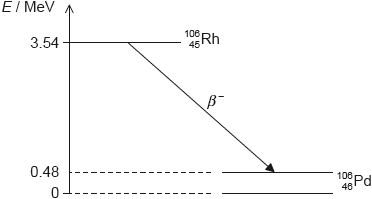
Rhodium-106 (\(_{\,\,\,45}^{106}{\text{Rh}}\)) decays into palladium-106 (\(_{\,\,\,46}^{106}{\text{Pd}}\)) by beta minus (β–) decay. The diagram shows some of the nuclear energy levels of rhodium-106 and palladium-106. The arrow represents the β– decay.
Bohr modified the Rutherford model by introducing the condition mvr = n\(\frac{h}{{2\pi }}\). Outline the reason for this modification.
Show that the speed v of an electron in the hydrogen atom is related to the radius r of the orbit by the expression
\[v = \sqrt {\frac{{k{e^2}}}{{{m_{\text{e}}}r}}} \]
where k is the Coulomb constant.
Using the answer in (b) and (c)(i), deduce that the radius r of the electron’s orbit in the ground state of hydrogen is given by the following expression.
\[r = \frac{{{h^2}}}{{4{\pi ^2}k{m_{\text{e}}}{e^2}}}\]
Calculate the electron’s orbital radius in (c)(ii).
Explain what may be deduced about the energy of the electron in the β– decay.
Suggest why the β– decay is followed by the emission of a gamma ray photon.
Calculate the wavelength of the gamma ray photon in (d)(ii).
Markscheme
the electrons accelerate and so radiate energy
they would therefore spiral into the nucleus/atoms would be unstable
electrons have discrete/only certain energy levels
the only orbits where electrons do not radiate are those that satisfy the Bohr condition «mvr = n\(\frac{h}{{2\pi }}\)»
[3 marks]
\(\frac{{{m_{\text{e}}}{v^2}}}{r} = \frac{{k{e^2}}}{{{r^2}}}\)
OR
KE = \(\frac{1}{2}\)PE hence \(\frac{1}{2}\)mev2 = \(\frac{1}{2}\frac{{k{e^2}}}{r}\)
«solving for v to get answer»
Answer given – look for correct working
[1 mark]
combining v = \(\sqrt {\frac{{k{e^2}}}{{{m_{\text{e}}}r}}} \) with mevr = \(\frac{h}{{2\pi }}\) using correct substitution
«eg \({m_e}^2\frac{{k{e^2}}}{{{m_{\text{e}}}r}}{r^2} = \frac{{{h^2}}}{{4{\pi ^2}}}\)»
correct algebraic manipulation to gain the answer
Answer given – look for correct working
Do not allow a bald statement of the answer for MP2. Some further working eg cancellation of m or r must be shown
[2 marks]
« r = \(\frac{{{{(6.63 \times {{10}^{ - 34}})}^2}}}{{4{\pi ^2} \times 8.99 \times {{10}^9} \times 9.11 \times {{10}^{ - 31}} \times {{(1.6 \times {{10}^{ - 19}})}^2}}}\)»
r = 5.3 × 10–11 «m»
[1 mark]
the energy released is 3.54 – 0.48 = 3.06 «MeV»
this is shared by the electron and the antineutrino
so the electron’s energy varies from 0 to 3.06 «MeV»
[3 marks]
the palladium nucleus emits the photon when it decays into the ground state «from the excited state»
[1 mark]
Photon energy
E = 0.48 × 106 × 1.6 × 10–19 = «7.68 × 10–14 J»
λ = «\(\frac{{hc}}{E} = \frac{{6.63 \times {{10}^{ - 34}} \times 3 \times {{10}^8}}}{{7.68 \times {{10}^{ - 14}}}}\) =» 2.6 × 10–12 «m»
Award [2] for a bald correct answer
Allow ECF from incorrect energy
[2 marks]
Examiners report
A planet has radius R. At a distance h above the surface of the planet the gravitational field strength is g and the gravitational potential is V.
State what is meant by gravitational field strength.
Show that V = –g(R + h).
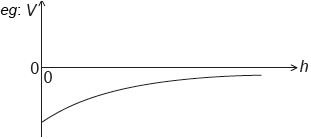
Draw a graph, on the axes, to show the variation of the gravitational potential V of the planet with height h above the surface of the planet.
A planet has a radius of 3.1 × 106 m. At a point P a distance 2.4 × 107 m above the surface of the planet the gravitational field strength is 2.2 N kg–1. Calculate the gravitational potential at point P, include an appropriate unit for your answer.
The diagram shows the path of an asteroid as it moves past the planet.
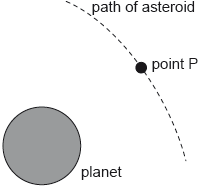
When the asteroid was far away from the planet it had negligible speed. Estimate the speed of the asteroid at point P as defined in (b).
The mass of the asteroid is 6.2 × 1012 kg. Calculate the gravitational force experienced by the planet when the asteroid is at point P.
Markscheme
the «gravitational» force per unit mass exerted on a point/small/test mass
[1 mark]
at height h potential is V = –\(\frac{{GM}}{{(R + h)}}\)
field is g = \(\frac{{GM}}{{{{(R + h)}^2}}}\)
«dividing gives answer»
Do not allow an answer that starts with g = –\(\frac{{\Delta V}}{{\Delta r}}\) and then cancels the deltas and substitutes R + h
[2 marks]
correct shape and sign
non-zero negative vertical intercept
[2 marks]
V = «–2.2 × (3.1 × 106 + 2.4 × 107) =» «–» 6.0 × 107 J kg–1
Unit is essential
Allow eg MJ kg–1 if power of 10 is correct
Allow other correct SI units eg m2s–2, N m kg–1
[1 mark]
total energy at P = 0 / KE gained = GPE lost
«\(\frac{1}{2}\)mv2 + mV = 0 ⇒» v = \(\sqrt { - 2V} \)
v = «\(\sqrt {2 \times 6.0 \times {{10}^7}} \) =» 1.1 × 104 «ms–1»
Award [3] for a bald correct answer
Ignore negative sign errors in the workings
Allow ECF from 6(b)
[3 marks]
ALTERNATIVE 1
force on asteroid is «6.2 × 1012 × 2.2 =» 1.4 × 1013 «N»
«by Newton’s third law» this is also the force on the planet
ALTERNATIVE 2
mass of planet = 2.4 x 1025 «kg» «from V = –\(\frac{{GM}}{{(R + h)}}\)»
force on planet «\(\frac{{GMm}}{{{{(R + h)}^2}}}\)» = 1.4 × 1013 «N»
MP2 must be explicit
[2 marks]
Examiners report
Part 2 Motion of a rocket
A rocket is moving away from a planet within the gravitational field of the planet. When the rocket is at position P a distance of 1.30×107m from the centre of the planet, the engine is switched off. At P, the speed of the rocket is 4.38×103ms–1.
At a time of 60.0 s later, the rocket has reached position Q. The speed of the rocket at Q is 4.25×103ms–1. Air resistance is negligible.
Outline, with reference to the energy of the rocket, why the speed of the rocket is changing between P and Q.
Estimate the average gravitational field strength of the planet between P and Q.
(i) An object is a distance r from the centre of a planet. Show that the minimum speed required to escape the gravitational field is equal to
\[\sqrt {2g'r} \]
where g′ is the gravitational field strength at distance r from the centre of a planet.
(ii) Discuss, using a calculation, whether the rocket at P can completely escape the gravitational field of the planet without further use of the engine.
A space station is in orbit at a distance r from the centre of the planet in (e)(i). A satellite is launched from the space station so as just to escape from the gravitational field of the planet. The launch takes place in the same direction as the velocity of the space station. Outline why the launch velocity relative to the space station can be less than your answer to (e)(i).
Markscheme
gravitational potential energy is being gained;
this is at the expense of kinetic energy (and speed falls);
\(\left( {{\rm{acceleration}} = \frac{{\left( {v - u} \right)}}{t} = \frac{{4.25 \times {{10}^3} - 4.38 \times {{10}^3}}}{{60}} = } \right)\left( - \right)2.17\left( {{\rm{m}}{{\rm{s}}^{ - 2}}} \right)\);
gravitational field strength = acceleration of rocket (=2.17 N kg–1); } (allow g = a in symbols)
or
computes potential difference from KE per unit mass change (5.61\( \times \)105),
computes distance travelled (0.259 Mm), uses \(g = \frac{{\left( - \right)\Delta V}}{{\Delta r}}\);
g=(\( - \))2.17(ms-2);
(i) \(\left( {{\rm{gravitational force}}} \right){\rm{ = }}mg'{\rm{ = }}\frac{{{\rm{GMm}}}}{{{r^2}}}\);
\(\left( {{\rm{kinetic energy}}} \right){\rm{ = }}\frac{{{\rm{m}}{{\rm{v}}^{\rm{2}}}}}{2} = \frac{{GMm}}{r}\);
\({v^2} = 2\frac{{GM}}{{{r^2}}}r\left( { = 2g'r} \right)\);
Award [0] for centripetal force argument as rocket is not in orbit.
(ii) calculation of speed at a relevant distance eg: \(\sqrt {2 \times g' \times 13 \times {{10}^6}} = 7500\left( {{\rm{m}}{{\rm{s}}^{ - 1}}} \right)\);
speed is less than this so will not escape; } (allow ECF from (d) which could lead to rocket able to escape)
Award [1 max] for use of g=9.81 and r which gives 16000 ms–1 .
the satellite has velocity/kinetic energy as it is orbiting with the space station;
Examiners report
The diagram shows a planet near two stars of equal mass M.
Each star has mass M=2.0×1030kg. Their centres are separated by a distance of 6.8×1011m. The planet is at a distance of 6.0×1011m from each star.
On the diagram above, draw two arrows to show the gravitational field strength at the position of the planet due to each of the stars.
Calculate the magnitude and state the direction of the resultant gravitational field strength at the position of the planet.
Markscheme
two arrows each along the line connecting the planet to its star AND directed towards each star
arrow lines straight and of equal length
Do not allow kinked, fuzzy curved lines.
\(g = \ll \frac{{GM}}{{{r^2}}} = \frac{{6.67 \times {{10}^{ - 11}} \times 2.0 \times {{10}^{30}}}}{{{{\left( {6.0 \times {{10}^{11}}} \right)}^2}}} \gg \) OR 3.7×10-4Nkg-1
\({g_{{\rm{net}}}} = \ll 2g\cos \theta = 2 \times 3.7 \times {10^{ - 4}} \times \frac{{\sqrt {{{6.0}^2} - {{3.4}^2}} }}{{6.0}} = \gg 6.1 \times {10^{ - 4}}{\rm{Nk}}{{\rm{g}}^{ - 1}}\)
directed vertically down «page» OR towards midpoint between two stars OR south
Allow rounding errors.
Examiners report
This question is about a probe in orbit.
A probe of mass m is in a circular orbit of radius r around a spherical planet of mass M.
State why the work done by the gravitational force during one full revolution of the probe is zero.
Deduce for the probe in orbit that its
(i) speed is \(v = \sqrt {\frac{{GM}}{r}} \).
(ii) total energy is \(E = - \frac{{GMm}}{{2r}}\).
It is now required to place the probe in another circular orbit further away from the planet. To do this, the probe’s engines will be fired for a very short time.
State and explain whether the work done on the probe by the engines is positive, negative or zero.
Markscheme
because the force is always at right angles to the velocity / motion/orbit is an equipotential surface;
Do not accept answers based on the displacement being zero for a full revolution.
(i) equating gravitational force \(\frac{{GMm}}{{{r^2}}}\);
to centripetal force \(\frac{{m{v^2}}}{r}\) to get result;
(ii) kinetic energy is \(\frac{{GMm}}{{2r}}\);
addition to potential energy −\(\frac{{GMm}}{{r}}\) to get result;
the total energy (at the new orbit) will be greater than before/is less negative;
hence probe engines must be fired to produce force in the direction of motion / positive work must be done (on the probe);
Award [1] for mention of only potential energy increasing.
Examiners report
This question is in two parts. Part 1 is about solar radiation and the greenhouse effect. Part 2 is about orbital motion.
Part 1 Solar radiation and the greenhouse effect
The following data are available.
Part 2 Orbital motion
A spaceship of mass m is moving at speed v in a circular orbit of radius r around a planet of mass M.
State the Stefan-Boltzmann law for a black body.
Deduce that the solar power incident per unit area at distance d from the Sun is given by
\(\frac{{\sigma {R^2}{T^4}}}{{{d^2}}}\).
Calculate, using the data given, the solar power incident per unit area at distance d from the Sun.
State two reasons why the solar power incident per unit area at a point on the surface of the Earth is likely to be different from your answer in (c).
The average power absorbed per unit area at the Earth’s surface is 240Wm–2. By treating the Earth’s surface as a black body, show that the average surface temperature of the Earth is approximately 250K.
Explain why the actual surface temperature of the Earth is greater than the value in (e).
(i) Identify the force that causes the centripetal acceleration of the spaceship.
(ii) Explain why astronauts inside the spaceship would feel “weightless”, even though there is a force acting on them.
Deduce that the speed of the spaceship is \(v = \sqrt {\frac{{GM}}{r}} \).
The table gives equations for the forms of energy of the orbiting spaceship.
The spaceship passes through a cloud of gas, so that a small frictional force acts on the spaceship.
(i) State and explain the effect that this force has on the total energy of the spaceship.
(ii) Outline the effect that this force has on the speed of the spaceship.
Markscheme
power/energy per second emitted is proportional to surface area;
and proportional to fourth power of absolute temperature / temperature in K;
Accept equation with symbols defined.
solar power given by \(4\pi {R^2}\sigma {T^4}\);
spreads out over sphere of surface area \(4\pi {d^2}\);
Hence equation given.
\(\left( {\frac{{\sigma {R^2}{T^4}}}{{{d^2}}} = } \right)\frac{{5.7 \times {{10}^{ - 8}} \times {{\left[ {7.0 \times {{10}^8}} \right]}^2} \times {{\left[ {5.8 \times {{10}^3}} \right]}^4}}}{{{{\left[ {1.5 \times {{10}^{11}}} \right]}^2}}}\);
=1.4×103(Wm-2);
Award [2] for a bald correct answer.
some energy reflected;
some energy absorbed/scattered by atmosphere;
depends on latitude;
depends on time of day;
depends on time of year;
depends on weather (eg cloud cover) at location;
power output of Sun varies;
Earth-Sun distance varies;
power radiated=power absorbed;
\(T = {}^4\sqrt {\frac{{240}}{{5.7 \times {{10}^{ - 8}}}}} \left( { = 250{\rm{K}}} \right)\);
Accept answers given as 260 (K).
radiation from Sun is re-emitted from Earth at longer wavelengths;
greenhouse gases in the atmosphere absorb some of this energy;
and radiate some of it back to the surface of the Earth;
(i) gravitational force / gravitational attraction / weight; (do not accept gravity)
(ii) astronauts and spaceship have the same acceleration;
acceleration is towards (centre of) planet;
so no reaction force between astronauts and spaceship;
or
astronauts and spaceships are both falling towards the (centre of the) planet;
at the same rate;
so no reaction force between astronauts and spaceship;
gravitational force equated with centripetal force / \(\frac{{GmM}}{{{r^2}}} = \frac{{m{v^2}}}{r}\);
\( \Rightarrow {v^2} = \frac{{GM}}{r} \Rightarrow \left( {v = \sqrt {\frac{{GM}}{r}} } \right)\);
(i) thermal energy is lost;
total energy decreases;
(ii) since E decreases, r also decreases;
as r decreases v increases / Ek increases so v increases;
Examiners report
The Stefan-Boltzmann law was poorly understood with few candidates stating that the absolute temperature is raised to the fourth power.
This question was poorly done with few candidates substituting the surface area of the sun or the surface area of a sphere at the Earth’s radius of orbit.
Despite not being able to state or manipulate the Stefan-Boltzmann law most candidates could substitute values into the expression and calculate a result.
This question was well answered at higher level.
To show the given value there is the requirement for an explanation of why the incident power absorbed by the Earth’s surface is equal to the power radiated by the Earth, few candidates were successful in this aspect. Although most could substitute into the Stefan-Boltzmann equation they needed to either show that the fourth root was used or to find the temperature to more significant figures than the value given.
A surprising number of candidates could not explain the greenhouse effect. A common misunderstanding was that the Earth reflected radiation into the atmosphere and that the atmosphere reflected the radiation back to the Earth.
(i) Most were able to state gravitational force, however a significant number stated gravity and consequently did not get the mark.
(ii) Many answers only discussed the astronauts and not the spaceship, missing points such as ‘falling at the same rate’ or ‘with the same acceleration’.
This was well answered with candidates able to adequately show in their explanation where the expression comes from.
ji) Most appreciated that the effect of the force would be to decrease the total energy.
jii) Very few appreciated that they should use the equations above to answer this part of the question. As a consequence, the most common answer discussed a decrease in kinetic energy and a decrease in speed.